Arno’s Engram keyboard layout

Engram v2.0 (“Engram”) is a key layout optimized for comfortable and efficient touch typing in English created by Arno Klein, with open source code to create other optimized key layouts. You can install the Engram v2.0 layout on Windows, macOS, and Linux or try it out online. An article is under review (see the preprint for an earlier (and superceded) version (v1.3) with description).

[See here for the Spanish version, engram-es]

Letters are optimally arranged according to ergonomics factors that promote reduction of lateral finger movements and more efficient typing of high-frequency letter pairs. The most common punctuation marks are logically grouped together in the middle columns and numbers are paired with mathematical and logic symbols (shown as pairs of default and Shift-key-accessed characters).

See below for a full description and comparisons with other key layouts.

Standard diagonal keyboard (default and Shift-key layers)

Standard keyboard

“Ergonomic” orthonormal keyboard (default and Shift-key layers)

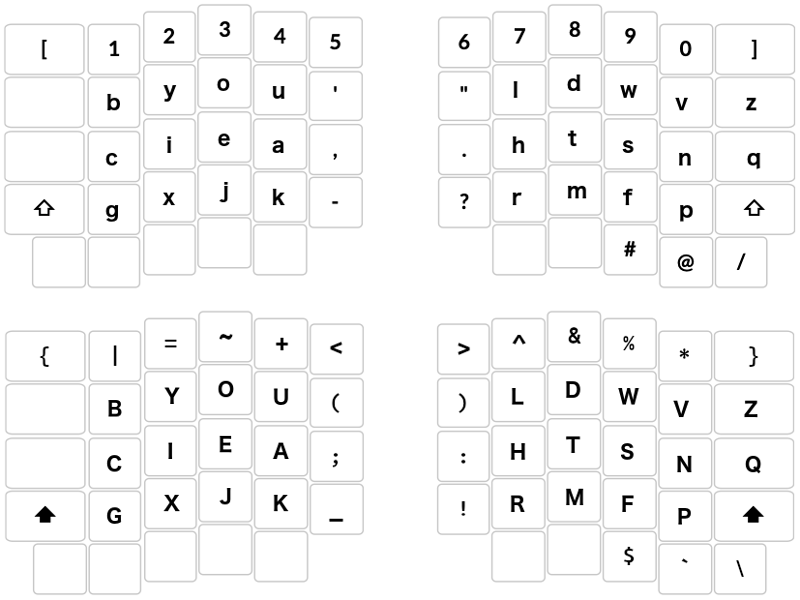
Orthonormal keyboard

     [{ 1| 2= 3~ 4+  5<  6>  7^ 8& 9% 0* ]} /\
        bB yY oO uU  '(  ")  lL dD wW vV zZ #$ @`
        cC iI eE aA  ,;  .:  hH tT sS nN qQ 
        gG xX jJ kK  -_  ?!  rR mM fF pP

Letter frequencies (Norvig, 2012), showing that the Engram layout emphasizes keys in the home row:

      B   Y   O   U           L   D   W   V    Z
      C   I   E   A           H   T   S   N    Q
      G   X   J   K           R   M   F   P

     53  59 272  97          145 136  60  38   3
    119 270 445 287          180 331 232 258   4
     67   8   6  19          224  90  86  76

(c) 2021 Arno Klein, MIT license

Contents

  1. Why a new key layout?
  2. How does Engram compare with other key layouts?
  3. Guiding criteria
  4. Summary of steps and results

Why a new key layout?

Personal history
In the future, I hope to include an engaging rationale for why I took on this challenge. Suffice to say I love solving problems, and I have battled repetitive strain injury ever since I worked on an old DEC workstation at the MIT Media Lab while composing my thesis back in the 1990s. I have experimented with a wide variety of human interface technologies over the years – voice dictation, one-handed keyboard, keyless keyboard, foot mouse, and ergonomic keyboards like the Kinesis Advantage and Ergodox keyboards with different key switches. While these technologies can significantly improve comfort and reduce strain, an optimized key layout can only help when typing on ergonomic or standard keyboards.

I have used different key layouts (Qwerty, Dvorak, Colemak, etc.) for communications and for writing and programming projects, and have primarily relied on Colemak for the last 10 years. I find that most to all of these key layouts:

While I used ergonomic principles outlined below and the accompanying code to help generate the Engram layout, I also relied on massive bigram frequency data for the English language. if one were to follow the procedure below and use a different set of bigram frequencies for another language or text corpus, they could create a variant of the Engram layout, say “Engram-French”, better suited to the French language.

Why “Engram”?
The name is a pun, referring both to “n-gram”, letter permutations and their frequencies that are used to compute the Engram layout, and “engram”, or memory trace, the postulated change in neural tissue to account for the persistence of memory, as a nod to my attempt to make this layout easy to remember.

How does Engram compare with other key layouts?

Below we compare the Engram layout with different prominent key layouts (Colemak, Dvorak, QWERTY, etc.) for some large, representative, publicly available data (all text sources are listed below and available on GitHub).

Engram Scoring Model scores (x100) for layouts, based on publicly available text data

Engram scores higher for all text and software sources than all other layouts according to its own scoring model (higher scores are better):

Layout Google bigrams Alice Memento Tweets_100K Tweets_20K Tweets_MASC Spoken_MASC COCA_blogs iweb Monkey Coder Rosetta
Engram 62.48 61.67 62.30 63.03 60.28 62.49 61.56 62.19 62.38 62.23 62.51 62.48
Halmak 62.40 61.60 62.23 62.93 60.26 62.43 61.51 62.13 62.31 62.16 62.46 62.40
Hieamtsrn 62.39 61.64 62.27 62.99 60.27 62.47 61.53 62.16 62.35 62.20 62.49 62.39
Norman 62.35 61.57 62.20 62.86 60.21 62.39 61.47 62.08 62.27 62.12 62.40 62.35
Workman 62.37 61.59 62.22 62.91 60.23 62.41 61.49 62.10 62.29 62.14 62.43 62.37
MTGap 2.0 62.32 61.59 62.21 62.88 60.22 62.39 61.49 62.09 62.28 62.13 62.42 62.32
QGMLWB 62.31 61.58 62.21 62.90 60.25 62.40 61.49 62.10 62.29 62.14 62.43 62.31
Colemak Mod-DH 62.36 61.60 62.22 62.90 60.26 62.41 61.49 62.12 62.30 62.16 62.44 62.36
Colemak 62.36 61.58 62.20 62.89 60.25 62.40 61.48 62.10 62.29 62.14 62.43 62.36
Asset 62.34 61.56 62.18 62.86 60.25 62.37 61.46 62.07 62.25 62.10 62.39 62.34
Capewell-Dvorak 62.29 61.56 62.17 62.86 60.20 62.36 61.47 62.06 62.24 62.10 62.37 62.29
Klausler 62.34 61.58 62.20 62.89 60.25 62.39 61.48 62.09 62.27 62.12 62.41 62.34
Dvorak 62.31 61.56 62.17 62.85 60.23 62.35 61.46 62.06 62.24 62.09 62.35 62.31
QWERTY 62.19 61.49 62.08 62.72 60.17 62.25 61.39 61.96 62.13 61.99 62.25 62.19

Keyboard Layout Analyzer (KLA) scores for the same text sources

The optimal layout score is based on a weighted calculation that factors in the distance your fingers moved (33%), how often you use particular fingers (33%), and how often you switch fingers and hands while typing (34%).

Engram scores highest for 7 of the 9 and second highest for 2 of the 9 text sources; Engram scores third and fourth highest for the two software sources, “Coder” and “Rosetta” (higher scores are better):

Layout Alice in Wonderland Memento screenplay 100K tweets 20K tweets MASC tweets MASC spoken COCA blogs iweb Monkey Coder Rosetta
Engram 70.13 57.16 64.64 58.58 60.24 64.39 69.66 68.25 67.66 46.81 47.69
Halmak 66.25 55.03 60.86 55.53 57.13 62.32 67.29 65.50 64.75 45.68 47.60
Hieamtsrn 69.43 56.75 64.40 58.95 60.47 64.33 69.93 69.15 68.30 46.01 46.48
Colemak Mod-DH 65.74 54.91 60.75 54.94 57.15 61.29 67.12 65.98 64.85 47.35 48.50
Norman 62.76 52.33 57.43 53.24 53.90 59.97 62.80 60.90 59.82 43.76 46.01
Workman 64.78 54.29 59.98 55.81 56.25 61.34 65.27 63.76 62.90 45.33 47.76
MTGAP 2.0 66.13 53.78 59.87 55.30 55.81 60.32 65.68 63.81 62.74 45.38 44.34
QGMLWB 65.45 54.07 60.51 56.05 56.90 62.23 66.26 64.76 63.91 46.38 45.72
Colemak 65.83 54.94 60.67 54.97 57.04 61.36 67.14 66.01 64.91 47.30 48.65
Asset 64.60 53.84 58.66 54.72 55.35 60.81 64.71 63.17 62.44 45.54 47.52
Capewell-Dvorak 66.94 55.66 62.14 56.85 57.99 62.83 66.95 65.23 64.70 45.30 45.62
Klausler 68.24 59.91 62.57 56.45 58.34 64.04 68.34 66.89 66.31 46.83 45.66
Dvorak 65.86 58.18 60.93 55.56 56.59 62.75 66.64 64.87 64.26 45.46 45.55
QWERTY 53.06 43.74 48.28 44.99 44.59 51.79 52.31 50.19 49.18 38.46 39.89

Keyboard Layout Analyzer consecutive same-finger key presses

KLA (and other) distance measures may not accurately reflect natural typing, so below is a more reliable measure of one source of effort and strain – the tally of consecutive key presses with the same finger for different keys. Engram scores lowest for 6 of the 11 texts, second lowest for two texts, and third or fifth lowest for three texts, two of which are software text sources (lower scores are better):

KLA (and other) distance measures may not accurately reflect natural typing, so below is a more reliable measure of one source of effort and strain – the tally of consecutive key presses with the same finger for different keys. Engram scores lowest for 6 of the 9 and second or third lowest for 3 of the 9 text sources, and third or fifth lowest for the two software text sources (lower scores are better):

Layout Alice Memento Tweets_100K Tweets_20K Tweets_MASC Spoken_MASC COCA_blogs iweb Monkey Coder Rosetta
Engram 216 11476 320406 120286 7728 3514 137290 1064640 37534 125798 5822
Halmak 498 13640 484702 170064 11456 5742 268246 2029634 68858 144790 5392
Hieamtsrn 244 12096 311000 119490 8316 3192 155674 1100116 40882 158698 7324
Norman 938 20012 721602 213890 16014 9022 595168 3885282 135844 179752 7402
Workman 550 13086 451280 136692 10698 6156 287622 1975564 71150 132526 5550
MTGap 2.0 226 14550 397690 139130 10386 6252 176724 1532844 58144 138484 7272
QGMLWB 812 17820 637788 189700 14364 7838 456442 3027530 100750 149366 8062
Colemak Mod-DH 362 10960 352578 151736 9298 4644 153984 1233770 47438 117842 5328
Colemak 362 10960 352578 151736 9298 4644 153984 1233770 47438 117842 5328
Asset 520 12519 519018 155246 11802 5664 332860 2269342 77406 140886 6020
Capewell-Dvorak 556 14226 501178 163878 12214 6816 335056 2391416 78152 151194 9008
Klausler 408 14734 455658 174998 11410 5212 257878 1794604 59566 135782 7444
Dvorak 516 13970 492604 171488 12208 5912 263018 1993346 64994 142084 6484

Inward roll frequencies

Here we tally the number of bigrams (in billions of instances from Norvig’s analysis of Google data) that engage inward rolls (little-to-index sequences), within the four columns of one hand, or any column across two hands. Engram scores second highest for 32 keys and highest for 24 keys, where the latter ensures that we are comparing Engram’s letters with letters in other layouts (higher scores are better):

Total inward roll frequency in billions

Layout             32 / 24 keys
Engram:          4.64 / 4.51
Halmak:          4.59 / 4.25
Hieamtsrn:       4.69 / 4.16
Norman:          3.99 / 3.61
Workman:         4.16 / 3.63
MTGap 2.0:       3.96 / 3.58
QGMLWB:          4.36 / 2.81
Colemak Mod-DH:  4.15 / 3.51
Colemak:         4.17 / 3.16
Asset:           4.03 / 3.05
Capewell-Dvorak: 4.39 / 3.66
Klausler:        4.42 / 3.52
Dvorak:          4.40 / 3.20
QWERTY:          3.62 / 2.13
Layout Year Website
Engram 2021 https://engram.dev
Halmak 2.2 2016 https://github.com/MadRabbit/halmak
Hieamtsrn 2014 https://mathematicalmulticore.wordpress.com/the-keyboard-layout-project/#comment-4976
Colemak Mod-DH 2014 https://colemakmods.github.io/mod-dh/
Norman 2013 https://normanlayout.info/
Workman 2010 https://workmanlayout.org/
MTGAP 2.0 2010 https://mathematicalmulticore.wordpress.com/2010/06/21/mtgaps-keyboard-layout-2-0/
QGMLWB 2009 http://mkweb.bcgsc.ca/carpalx/?full_optimization
Colemak 2006 https://colemak.com/
Asset 2006 http://millikeys.sourceforge.net/asset/
Capewell-Dvorak 2004 http://michaelcapewell.com/projects/keyboard/layout_capewell-dvorak.htm
Klausler 2002 https://web.archive.org/web/20031001163722/http://klausler.com/evolved.html
Dvorak 1936 https://en.wikipedia.org/wiki/Dvorak_keyboard_layout
QWERTY 1873 https://en.wikipedia.org/wiki/QWERTY
Text source Information
“Alice in Wonderland” Alice in Wonderland (Ch.1)
“Memento screenplay” Memento screenplay
“100K tweets” 100,000 tweets from: Sentiment140 dataset training data
“20K tweets” 20,000 tweets from Gender Classifier Data
“MASC tweets” MASC tweets (cleaned of html markup)
“MASC spoken” MASC spoken transcripts (phone and face-to-face: 25,783 words)
“COCA blogs” Corpus of Contemporary American English blog samples
“Rosetta” “Tower of Hanoi” (programming languages A-Z from Rosetta Code)
“Monkey text” Ian Douglas’s English-generated monkey0-7.txt corpus
“Coder text” Ian Douglas’s software-generated coder0-7.txt corpus
“iweb cleaned corpus” First 150,000 lines of Shai Coleman’s iweb-corpus-samples-cleaned.txt

Reference for Monkey and Coder texts: Douglas, Ian. (2021, March 28). Keyboard Layout Analysis: Creating the Corpus, Bigram Chains, and Shakespeare’s Monkeys (Version 1.0.0). Zenodo. http://doi.org/10.5281/zenodo.4642460

Guiding criteria 

1.  Assign letters to keys that don't require lateral finger movements.
2.  Promote alternating between hands over uncomfortable same-hand transitions.
3.  Assign the most common letters to the most comfortable keys.
4.  Arrange letters so that more frequent bigrams are easier to type.
5.  Promote little-to-index-finger roll-ins over index-to-little-finger roll-outs.
6.  Balance finger loads according to their relative strength.
7.  Avoid stretching shorter fingers up and longer fingers down.
8.  Avoid using the same finger.
9.  Avoid skipping over the home row.
10. Assign the most common punctuation to keys in the middle of the keyboard.
11. Assign easy-to-remember symbols to the Shift-number keys.

Factors used to compute the Engram layout

Summary of steps and results

We will assign letters to keys by choosing the arrangement with the highest score according to our scoring model. However, there are over four hundred septillion, or four hundred trillion trillion (26! = 403,291,461,126,605,635,584,000,000, or 4.032914611 E+26) possible arrangements of 26 letters (24! = 6.204484017 E+23), so we will arrange the letters in four steps, based on ergonomics principles. These consist of (Step 1) assigning the eight most frequent letters to different keys, optimizing assignment of the remaining (Step 2) eight most frequent letters, and (Step 3) eight least frequent letters (besides Z and Q), and (Step 4) exchanging letters.

Step 1: Define the shape of the key layout to minimize lateral finger movements

We will assign 24 letters to 8 columns of keys separated by two middle columns reserved for punctuation. These 8 columns require no lateral finger movements when touch typing, since there is one column per finger. The most comfortable keys include the left and right home rows (keys 5-8 and 17-20), the top-center keys (2,3 and 14,15) that allow the longer middle and ring fingers to uncurl upwards, as well as the bottom corner keys (9,12 and 21,24) that allow the shorter fingers to curl downwards. We will assign the two least frequent letters, Z and Q (or J), to the two hardest-to-reach keys lying outside the 24-key columns in the upper right (25 and 26):

    Left:            Right:
 1  2  3  4       13 14 15 16 25
 5  6  7  8       17 18 19 20 26
 9 10 11 12       21 22 23 24

We will consider the most comfortable keys to be those typed by either hand on the home row, by the ring and middle finger above the home row, and by the index and little finger below the home row, with a preference for the strongest (index and middle) fingers:

 -  2  3  -        - 14 15  -  
 5  6  7  8       17 18 19 20  
 9  -  - 12       21  -  - 24

Step 2: Arrange the most frequent letters based on comfort and bigram frequencies

In prior experiments using the methods below, all vowels consistently automatically clustered together. Below, we will arrange vowels on one side and the most frequent consonants to the other side to encourage balance and alternation across hands. Since aside from the letters Z and Q there is symmetry across left and right sides, we will decide later which side the vowels and which side the most frequent consonants should go.

Vowels

E, T, A, O, I, N, S, R, H, L, D, C, U, M, F, P, G, W, Y, B, V, K, X, J, Q, Z

The highest frequency bigrams that contain two vowels are listed below in bold, with more than 10 billion instances in Peter Norvig’s analysis of Google data:

OU, IO, EA, IE, AI, IA, EI, UE, UA, AU, UI, OI, EO, OA, OE

 OU  24,531,132,241
 IO  23,542,263,265
 EA  19,403,941,063
 IE  10,845,731,320
 AI   8,922,759,715
 IA   8,072,199,471   
 EI   5,169,898,489
 UE   4,158,448,570       
 UA   3,844,138,094   
 AU   3,356,322,923
 UI   2,852,182,384
 OI   2,474,275,212
 EO   2,044,268,477
 OA   1,620,913,259
 OE   1,089,254,517

We will assign the most frequent vowels with over 100 billion instances in Norvig’s analysis (E=445,A=331,O=272,I=270) to four of the six most comfortable keys on the left side of the keyboard (keys 2,3,5,6,7,8). We will assign the letter E, the most frequent in the English language, to either of the strongest (index and middle) fingers on the home row, and assign the other three vowels such that (1) the home row keys typed by the index and middle fingers are not left vacant, and any top-frequency bigram (more than 10 billion instances in Norvig’s analysis) (2) does not use the same finger and (3) reads from left to right (ex: EA, not AE) for ease of typing (inward roll from little to index finger vs. outward roll from index to little finger). These constraints lead to three arrangements of the four vowels:

- - O -    - - O -    - - - -    
- I E A    I - E A    I O E A
- - - -    - - - -    - - - -

Consonants

On the right side of the keyboard, we will assign four of the five most frequent consonants (with over 5% or 150 billion instances in Norvig’s analysis: T=331, N=258, S=232, R=224, and H=180) to the four home row keys. We will assign the letter T, the most frequent consonant in the English language, to either of the strongest (index and middle) fingers on the home row. As with the left side, letters are placed so that top-frequency bigrams read from right to left (ex: HT, not TH) for ease of typing. The top-frequency bigrams (more than 10 billion instances in Norvig’s analysis) include: TH, ND, ST, NT, CH, NS, CT, TR, RS, NC, and RT (below 10 billion instances these bigrams start to occur in reverse, such as RT and TS):

 TH 100,272,945,963  3.56% 
 ND  38,129,777,631  1.35%
 ST  29,704,461,829  1.05%
 NT  29,359,771,944  1.04%
 CH  16,854,985,236  0.60%
 NS  14,350,320,288   
 CT  12,997,849,406
 TR  12,006,693,396       
 RS  11,180,732,354   
 NC  11,722,631,112
 RT  10,198,055,461

The above constraints lead to five arrangements of the consonants:

- - - -    - - - -    - - - -    - - - -    - - - -
R T S N    H T S N    H T S R    H T N R    T S N R
- - - -    - - - -    - - - -    - - - -    - - - -

We will assign the fifth consonant to a vacant key on the left home row if there is a vacancy, otherwise to the key below the right index finger (any other assignment requires the same finger to type a high-frequency bigram). The resulting 20 initial layouts, each with 15 unassigned keys, are represented below with the three rows on the left and right side of the keyboard as a linear string of letters, with unassigned keys denoted by “-”.

--O- HIEA ----    ---- RTSN ----
--O- RIEA ----    ---- HTSN ----
--O- NIEA ----    ---- HTSR ----
--O- SIEA ----    ---- HTNR ----
--O- IHEA ----    ---- RTSN ----
--O- IREA ----    ---- HTSN ----
--O- INEA ----    ---- HTSR ----
--O- ISEA ----    ---- HTNR ----
--O- -IEA ----    ---- RTSN H---
--O- -IEA ----    ---- HTSN R---
--O- -IEA ----    ---- HTSR N---
--O- I-EA ----    ---- RTSN H---
--O- I-EA ----    ---- HTSN R---
--O- I-EA ----    ---- HTSR N---
---- IOEA ----    ---- RTSN H---
---- IOEA ----    ---- HTSN R---
---- IOEA ----    ---- HTSR N---
--O- HIEA ----    ---- TSNR ----
--O- IHEA ----    ---- TSNR ----

Step 3: Optimize assignment of the remaining letters

We want to assign letters to the 17 unassigned keys in each of the above 20 layouts based on our scoring model. That would mean scoring all possible arrangements for each layout and choosing the arrangement with the highest score, but since there are over 355 trillion (17!) possible ways of arranging 17 letters, we will break up the assignment into two stages for the most frequent and least frequent remaining letters.

Most frequent letters

We will compute scores for every possible arrangement of the seven most frequent of the remaining letters (in bold below) assigned to vacancies among the most comfortable sixteen keys.

E, T, A, O, I, N, S, R, H, L, D, C, U, M, F, P, G, W, Y, B, V, K, X, J, Q, Z

    Left:            Right:
 -  2  3  -        - 14 15  -
 5  6  7  8       17 18 19 20
 9  -  - 12       21  -  - 24

Since there are 5,040 (7!) possible combinations of eight letters for each of the 21 layouts, we need to score and evaluate 105,840 layouts. To score each arrangement of letters, we construct a frequency matrix where we multiply a matrix containing the frequency of each ordered pair of letters (bigram) by our flow and strength matrices to compute a score.

Least frequent letters

Next we will compute scores for every possible (40,320 = 8!) arrangement of the least frequent eight letters (in bold below, besides Z and Q) in the remaining keys, after substituting in the 21 results of the above for an additional 846,720 layouts:

E, T, A, O, I, N, S, R, H, L, D, C, U, M, F, P, G, W, Y, B, V, K, X, J, Q, Z

    Left:            Right:
 1  -  -  4       13  -  - 16
 -  -  -  -        -  -  -  -
 - 10 11  -        - 22 23  -

Further optimize layouts by exchanging more letters

If we relax the above fixed initializations and permit further exchange of letters, then we can search for even higher-scoring layouts. As a final optimization step we exchange letters, eight keys at a time (8! = 40,320) selected twice in 14 different ways, in each of the above 21 layouts, to score a total of 23,708,160 more combinations. We allow the following keys to exchange letters:

1. Top rows
2. Bottom rows
3. Top and bottom rows on the right side
4. Top and bottom rows on the left side
5. Top right and bottom left rows
6. Top left and bottom right rows
7. Center of the top and bottom rows on both sides
8. The eight corners
9. Left half of the top and bottom rows on both sides
10. Right half of the top and bottom rows on both sides
11. Left half of non-home rows on the left and right half of the same rows on the right
12. Right half of non-home rows on the left and left half of the same rows on the right
13. Top center and lower sides
14. Top sides and lower center
15. Repeat 1-14

Engram Scoring Model

Our optimization algorithm finds every permutation of a given set of letters, maps these letter permutations to a set of keys, and ranks these letter-key mappings according to a score reflecting ease of typing key pairs and frequency of letter pairs (bigrams). The score is the average of the scores for all possible bigrams in this arrangement. The score for each bigram is a product of the frequency of occurrence of that bigram, the frequency of each of the bigram’s characters, and flow, strength (and optional speed) factors for the key pair.

Factors to penalize strenuous key transitions

Direction:

- outward = 0.9: outward roll of fingers from the index to little finger (same hand)

Dexterity:

- side_above_3away = 0.9
    - index and little finger type two keys, one or more rows apart (same hand)
- side_above_2away = 0.9^2 = 0.81
    - index finger types key a row or two above ring finger key, or
    - little finger types key a row or two above middle finger key (same hand)
- side_above_1away = 0.9^3 = 0.729
    - index finger types key a row or two above middle finger key, or
    - little finger types key a row or two above ring finger key (same hand)
- middle_above_ring = 0.9
    - middle finger types key a row or two above ring finger key (same hand)
- ring_above_middle = 0.9^3 = 0.729
    - ring finger types key a row or two above middle finger key (same hand)
- lateral = 0.9
    - lateral movement of (index or little) finger outside of 8 vertical columns

Distance:

- skip_row_3away = 0.9       
    - index and little fingers type two keys that skip over home row (same hand)
    - (e.g., one on bottom row, the other on top row)
- skip_row_2away = 0.9^3 = 0.729
    - little and middle or index and ring fingers type two keys that skip over home row (same hand)
- skip_row_1away = 0.9^5 = 0.59049
    - little and ring or middle and index fingers type two keys that skip over home row (same hand)

Repetition:

- skip_row_0away = 0.9^4 = 0.6561
    - same finger types two keys that skip over home row
- same_finger = 0.9^5 = 0.59049
    - use same finger again for a different key
    - cannot accompany outward, side_above, or adjacent_shorter_above

Strength: Accounted for by the strength matrix (minimum value for the little finger = 0.9)

Step 4: Evaluate winner against other optimized layouts

After assigning letters Z and Q to upper right keys outside of the home blocks and testing left/right side swap of all letters, the winning layout is:

B Y O U  L D W V Z
C I E A  H T S N Q
G X J K  R M F P

We ran tests on the winning layout:

1. Evaluate optimized layouts using interkey speed estimates   
2. Evaluate variants of the candidate winner using interkey speed estimates
3. Test sensitivity of the candidate winner to the scoring parameters

For test 1, we rescored all of the 20 top-scoring layouts optimized from the 20 initialized layouts, and replaced the factor matrix with the inter-key speed matrix. The same two layouts that tied for first place do so again.

For test 2, we rescored all of the 5,040 variants of the candidate winner that were tied for first place, replacing the factor matrix with the interkey speed matrix. The candidate winner scored highest.

For test 3, we ran a test on the variants of the candidate winner layout to see how robust they are to removal of scoring parameters. We removed each of the 11 scoring parameters one by one and ranked the new scores for the variants. The candidate winner scored highest for 8 of the 11 cases, and second highest for two other cases, demonstrating that this layout is not sensitive to individual parameters.

Step 5. Arrange non-letter characters in easy-to-remember places

Now that we have all 26 letters accounted for, we turn our attention to non-letter characters, taking into account frequency of punctuation and ease of recall.

Frequency of punctuation marks

Frequency:

         Sun:     Malik:   Ruhlen:    Cook:            Xah:
          /1M   N-gram %   /10,000   /1,000       All%  JS%   Py%

.    42840.02      1.151       535     65.3       6.6   9.4  10.3
,    44189.96                  556     61.6       5.8   8.9   7.5
"                  2.284        44     26.7       3.9   1.6   6.2
'     2980.35      0.200        40     24.3       4.4   4.0   8.6
-     9529.78      0.217        21     15.3       4.1   1.9   3.0
()    4500.81      0.140         7                7.4   9.8   8.1
;     1355.22      0.096        22      3.2       3.8   8.6
z                  0.09                   -         -
:     3221.82      0.087        11      3.4       3.5   2.8   4.7
?     4154.78      0.032        14      5.6       0.3
/                  0.019                          4.0   4.9   1.1
!     2057.22      0.013         3      3.3       0.4
_                  0.001                         11.0   2.9  10.5

Add punctuation keys and number keys

We will assign the most frequent punctuation according to Sun, et al (2018) to the six keys in the middle two columns: . , “ ‘ - ? ; : () ! _

        B Y O U   '  "   L D W V Z
        C I E A   ,  .   H T S N Q
        G X J K   -  ?   R M F P

We will use the Shift key to group similar punctuation marks (separating and joining marks in the left middle column and closing marks in the right middle column):

        B Y O U  '(  ")  L D W V Z #$ @`
        C I E A  ,;  .:  H T S N Q
        G X J K  -_  ?!  R M F P

Separating marks (left): The comma separates text in lists; the semicolon can be used in place of the comma to separate items in a list (especially if these items contain commas); open parenthesis sets off an explanatory word, phrase, or sentence.

Joining marks (left): The apostrophe joins words as contractions; the hyphen joins words as compounds; the underscore joins words in cases where whitespace characters are not permitted (such as in variables or file names).

Closing marks (right): A sentence usually ends with a period, question mark, or exclamation mark. The colon ends one statement but precedes the following: an explanation, quotation, list, etc. Double quotes and close parenthesis closes a word, clause, or sentence separated by an open parenthesis.

Number keys: The numbers are flanked to the left and right by [square brackets], and {curly brackets} accessed by the Shift key. Each of the numbers is paired with a mathematical or logic symbol accessed by the Shift key:

{ | = ~ +   <  >   ^ & % * } \
[ 1 2 3 4   5  6   7 8 9 0 ] /

1: | (vertical bar or "pipe" represents the logical OR operator: 1 stroke, looks like the number one)
2: = (equal: 2 strokes, like the Chinese character for "2")
3: ~ (tilde: "almost equal", often written with 3 strokes, like the Chinese character for "3")
4: + (plus: has four quadrants; resembles "4")
5 & 6: < > ("less/greater than"; these angle brackets are directly above the other bracket keys)
7: ^ (caret for logical XOR operator as well as exponentiation; resembles "7")
8: & (ampersand: logical AND operator; resembles "8")
9: % (percent: related to division; resembles "9")
0: * (asterisk: for multiplication; resembles "0")

The three remaining keys in many common keyboards (flanking the upper right hand corner Backspace key) are displaced in special keyboards, such as the Kinesis Advantage and Ergodox. For the top right key, we will assign the forward slash and backslash: / \. For the remaining two keys, we will assign two symbols that in modern usage have significance in social media: the hash/pound sign and the “at sign”. The hash or hashtag identifies digital content on a specific topic (the Shift key accesses the dollar sign). The “at sign” identifies a location or affiliation (such as in email addresses) and acts as a “handle” to identify users in popular social media platforms and online forums.

The resulting Engram layout:

     [{ 1| 2= 3~ 4+  5<  6>  7^ 8& 9% 0* ]} /\
        bB yY oO uU  '(  ")  lL dD wW vV zZ #$ @`
        cC iI eE aA  ,;  .:  hH tT sS nN qQ
        gG xX jJ kK  -_  ?!  rR mM fF pP